Digital

The digital module in the Qili SDK facilitates the construction and simulation of digital quantum systems. It is composed of the following primary components:

  • gates: A collection of quantum gates and tools for gate construction.

  • Circuit: A class to create and manage digital quantum circuits.

  • ansatz: Predefined circuits that can serve as Ansätze.

Gates

This submodule provides the necessary components to define and manipulate quantum gates for use in digital quantum circuits.

Simple Gates

Use these constructors to apply standard single- and two-qubit operations:

  • X(qubit: int) Pauli X (bit-flip) on the specified qubit.

  • Y(qubit: int) Pauli Y (bit-and-phase-flip).

  • Z(qubit: int) Pauli Z (phase-flip).

  • H(qubit: int) Hadamard: creates superposition.

  • I(qubit: int) Identity gate: leaves the qubit unchanged.

  • S(qubit: int) Phase gate (π/2 rotation about Z).

  • T(qubit: int) T gate (π/4 rotation about Z).

  • RX(qubit: int, theta: float) Rotation by angle theta around X.

  • RY(qubit: int, theta: float) Rotation by angle theta around Y.

  • RZ(qubit: int, phi: float) Rotation by angle phi around Z.

  • U1(qubit: int, *, phi: float) Phase shift equivalent to RZ plus global phase.

  • U2(qubit: int, *, phi: float, gamma: float) π/2 Y-rotation sandwiched by Z-rotations.

  • U3(qubit: int, *, theta: float, phi: float, gamma: float) General single-qubit unitary: RZ-RY-RZ decomposition.

  • SWAP(a: int, b: int) Exchanges the states of qubits a and b.

  • CNOT(control: int, target: int) Controlled-X: flips target if control is |1⟩.

  • CZ(control: int, target: int) Controlled-Z: applies Z on target if control is |1⟩.

  • M(*qubits: int) Measures the listed qubits in the computational basis.

Controlled Gates

Any basic gate can be turned into a controlled gate using the Controlled class:

from qilisdk.digital.gates import Controlled, Y

controlled_y = Controlled(0, basic_gate=Y(1))

Adjoint Gates

You can create the Hermitian conjugate (dagger) of a gate using the Adjoint class:

from qilisdk.digital.gates import Adjoint, Y

adjoint_y = Adjoint(basic_gate=Y(1))

Exponential Gates

To apply a gate as an exponential operator, use the Exponential class:

from qilisdk.digital.gates import Exponential, Y

exp_y = Exponential(basic_gate=Y(1))

Circuits

Quantum circuits can be built using the Circuit class. You can sequentially add gates to define the circuit:

Initialization

from qilisdk.digital import Circuit

# Create a 3-qubit circuit
circuit = Circuit(nqubits=3)

Adding Gates

from qilisdk.digital import H, CNOT

circuit.add(H(0))  # Hadamard on qubit 0
circuit.add(CNOT(0, 1))  # CNOT: control 0 → target 2
circuit.draw()

Parameterized Circuits

Circuits can include parameterized gates. Adding them is similar to regular gates:

from qilisdk.digital import RX
import numpy as np

circuit.add(RX(0, theta=np.pi))

You can retrieve the current parameter:

print("Initial Parameters:", circuit.get_parameters())

Output:

Initial Parameters: {'RX(0)_theta_0': 3.141592653589793}

You can also retrieve the current parameter values only:

print("Initial parameter values:", circuit.get_parameter_values())

Output:

Initial parameter values: [3.141592653589793]

To update parameter by key:

circuit.set_parameters({"RX(0)_theta_0": 2 * np.pi})

To update parameter by value:

circuit.set_parameter_values([2 * np.pi])

Warning

The order of parameters in the list passed to set_parameter_values must match the order in which the gates were added to the circuit.

Visualization

Use draw() to render a circuit with Matplotlib. By default, the renderer applies the library’s built-in styling (including the bundled default font if available). You can bypass all defaults by passing a custom CircuitStyle, which confines styling to the specific call without modifying global Matplotlib settings.

from qilisdk.digital import Circuit, H, CNOT

circuit = Circuit(num_qubits=3)
circuit.add(H(0))
circuit.add(CNOT(0, 2))

# Render in a window
circuit.draw()

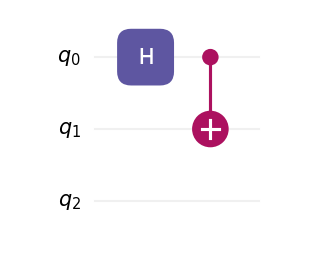
Saving to a file

# Save as SVG (use .png, .pdf, etc. as needed)
circuit.draw(filepath="my_circuit.svg")

Custom styling with CircuitStyle

Create a style object to control theme, fonts, spacing, DPI, labels, and more. Passing this object to draw overrides the library defaults for this call. You can also change if the order of the draw follows the order they are added in or if it compacts the layers as much as possible changing the patameter layout to “normal” (default) or “compact” respectively.

from qilisdk.digital import Circuit, H, CNOT
from qilisdk.utils.visualization import CircuitStyle, light, dark

circuit = Circuit(3)
circuit.add(H(0))
circuit.add(CNOT(0, 2))

# Example 1: dark theme, larger text, higher DPI
style_dark = CircuitStyle(
    theme=dark,
    dpi=200,
    fontsize=12,
    title="Teleportation (fragment)",
)
circuit.draw(style=style_dark)

# Example 2: use a system font family and bypass the bundled font
style_font = CircuitStyle(
    theme=light,
    fontfname=None,                         # do not force a specific TTF file
    fontfamily=["DejaVu Sans", "Arial"],    # fallback list
    fontsize=11,
)
circuit.draw(style=style_font, filepath="circuit_custom_font.png")

# Example 3: adjust layout spacing
compact = CircuitStyle(
    theme=dark,
    wire_sep=0.45,      # vertical distance between wires (inches)
    layer_sep=0.45,     # horizontal distance between layers (inches)
    gate_margin=0.10,   # side margin inside each layer cell (inches)
    label_pad=0.08,     # left padding for wire labels (inches)
    layout="compact",   # compresses the circuit whenever possible
    title="Compact layout",
)
circuit.draw(style=compact)

Note

CircuitStyle fields map directly to the renderer’s layout and font configuration. In particular, you can switch fonts in two ways: (1) provide a specific font file via fontfname="/path/to/MyFont.ttf"; or (2) set fontfname=None and choose a family list with fontfamily=[...] to use system-resolved fonts. Both approaches only affect the current draw call.

Ansatz

The ansatz submodule provides ready-to-use circuit templates (Ansätze). For example:

HardwareEfficientAnsatz

HardwareEfficientAnsatz is a hardware-efficient ansatz tailored to quantum device topologies. Configuration options:

  • layers: Number of repeating layers of gates.

  • connectivity: - Circular: Qubits form a ring. - Linear: Qubits are connected linearly. - Full: All-to-all connectivity.

  • one_qubit_gate: Choose the parameterized single-qubit gate (e.g., U1, U2, U3).

  • two_qubit_gate: Choose the two-qubit interaction type (e.g., CNOT, CZ).

  • structure: - grouped: Applies all single-qubit gates first, followed by all two-qubit gates. - interposed: Interleaves single and two-qubit gates.

Example

from qilisdk.digital.ansatz import HardwareEfficientAnsatz
from qilisdk.digital import U3, CNOT


ansatz = HardwareEfficientAnsatz(
    nqubits=4,
    layers=3,
    connectivity="Circular",
    one_qubit_gate=U3,
    two_qubit_gate=CNOT,
    structure="Interposed"
)

Parameter Utilities

Circuits collect the symbolic parameters contributed by each gate. Beyond the quick examples above, you can query names, current values, and bounds, or update them selectively:

import numpy as np

from qilisdk.common.variables import Parameter
from qilisdk.digital import Circuit, RX, RZ

circuit = Circuit(nqubits=2)
theta = Parameter("theta", value=np.pi / 4, bounds=(0.0, np.pi))

circuit.add(RX(0, theta=theta))
circuit.add(RZ(1, phi=np.pi / 2))

print(circuit.get_parameter_names())   # ['RX(0)_theta_0', 'RZ(1)_phi_1']
print(circuit.get_parameters())        # {'RX(0)_theta_0': 0.785..., 'RZ(1)_phi_1': 1.570...}
print(circuit.get_parameter_bounds())  # {'RX(0)_theta_0': (0.0, 3.1415...), 'RZ(1)_phi_1': (None, None)}

circuit.set_parameter_bounds({"RX(0)_theta_0": (0.1, np.pi / 2)})
circuit.set_parameters({"RX(0)_theta_0": np.pi / 3})
circuit.set_parameter_values([np.pi / 3, np.pi / 2])

These helpers make it straightforward to plug the circuit into classical optimization loops while keeping parameter metadata synchronized.

Gate Modifiers and Measurement

Every base gate inherits convenience methods to produce derived operations without manually instantiating Controlled, Adjoint, or Exponential. The measurement gate M lets you add classical readout at the end of the circuit.

import numpy as np

from qilisdk.digital import Circuit, H, X, RX, M

circuit = Circuit(2)
circuit.add(H(0))

# Promote a basic gate to a controlled version on the fly
circuit.add(X(1).controlled(0))

# Generate adjoint / exponential variants, preserving parameters
circuit.add(RX(1, theta=np.pi / 4).adjoint())
circuit.add(RX(0, theta=np.pi / 3).exponential())

# Record measurement results for both qubits
circuit.add(M(0, 1))

Controlled gates validate that control and target qubits are disjoint, and all wrapper gates forward parameter accessors to the underlying operation.